11. 盛最多水的容器
type
status
date
slug
summary
tags
category
difficulty
icon
password
11. 盛最多水的容器
给定一个长度为
n 的整数数组 height 。有 n 条垂线,第 i 条线的两个端点是 (i, 0) 和 (i, height[i]) 。找出其中的两条线,使得它们与
x 轴共同构成的容器可以容纳最多的水。返回容器可以储存的最大水量。
说明:你不能倾斜容器。
示例 1:
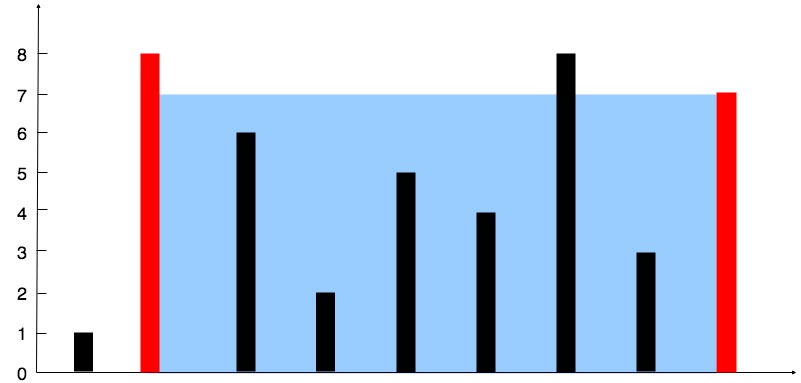
示例 2:
提示:
n == height.length
2 <= n <= 105
0 <= height[i] <= 104
解题思路
这道题可以使用双指针法求解。我们需要找出两条垂线,使它们与x轴构成的容器能够盛装最多的水。
算法流程
- 初始化:
- 设置左指针 i 指向数组开头(i = 0)
- 设置右指针 j 指向数组末尾(j = n-1)
- 初始化结果变量 res = 0
- 双指针移动策略:
- 计算当前面积:width = j - i(两线距离),height = min(height[i], height[j])(较短的线)
- 更新最大面积:res = max(res, width * height)
- 移动较短的那条线对应的指针:
- 如果 height[i] < height[j],移动左指针 i++
- 否则移动右指针 j--
为什么这样做是对的?
- 面积由两个因素决定:两条垂线的距离(宽度)和较短的垂线高度(高度)。
- 初始时,两指针距离最远,宽度最大。
- 我们总是移动较短的那条垂线对应的指针,因为:
- 如果移动较长的线,宽度减小,而高度不可能超过较短的线
- 移动较短的线,虽然宽度减小,但可能找到更高的线,从而得到更大的面积
复杂度分析
- 时间复杂度:O(n),其中 n 是数组的长度。指针移动n次即可完成遍历。
- 空间复杂度:O(1),只需要常数级别的额外空间。
- 作者:Episkey
- 链接:https://episkey.top/article/container-with-most-water
- 声明:本文采用 CC BY-NC-SA 4.0 许可协议,转载请注明出处。






